算法学习—回溯法

1、回溯法的概念

回溯法，顾名思义就是不断地重复枚举结果集，直到找到我们所要的结果。这种思想类似于暴力搜索，但是又与暴力搜索有着不同，回溯法使用了剪枝函数，除去了一些错误的解法。
回溯法在搜索的过程中，如果发现这一步的结果不符合结果的要求，则会放弃下面的查找，回溯到上一步，更换一种新的查找方式，它其实是一种选优搜索，根据选优条件逐步搜索，以达到目标。回溯法中满足回溯条件的点我们称为 “回溯点”。
在一些复杂问题，或者是比较大规模的问题中，我们都可以使用回溯法来解决，所以回溯法也有着“通用解题方法”的美称。

2、基本思想

回溯法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条新的路尝试。回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题。

3、解题步骤

1.定义一个解空间，它包含问题的解；
2.利用适于搜索的方法组织解空间；
3.利用深度优先法搜索解空间；
4.利用限界函数避免移动到不可能产生解的子空间。

4、实际例子

4.1、全排列问题

leetcode-46

题目：给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以 按任意顺序 返回答案。

示例1：

1 2	输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例2：

1 2	输入：nums = [0,1] 输出：[[0,1],[1,0]]

提示：

1
2
3

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

解题思路：

这个全排列问题是一个典型的回溯法问题。从左到右，我们不断尝试所有可能的结果，如果有出现重复的结果就除去，

我们定义递归函数 backtrack(first,output) 表示从左往右填到第 first 个位置，当前排列为 output。那么整个递归函数分为两个情况：

如果 first=n，说明我们已经填完了 n 个位置（注意下标从 0 开始），找到了一个可行的解，我们将 output 放入答案数组中，递归结束。
如果 first<n，我们要考虑这第 first 个位置我们要填哪个数。根据题目要求我们肯定不能填已经填过的数，因此很容易想到的一个处理手段是我们定义一个标记数组 vis 来标记已经填过的数，那么在填第 first 个数的时候我们遍历题目给定的 n 个数，如果这个数没有被标记过，我们就尝试填入，并将其标记，继续尝试填下一个位置，即调用函数 backtrack(first+1,output)。回溯的时候要撤销这一个位置填的数以及标记，并继续尝试其他没被标记过的数。

示例图：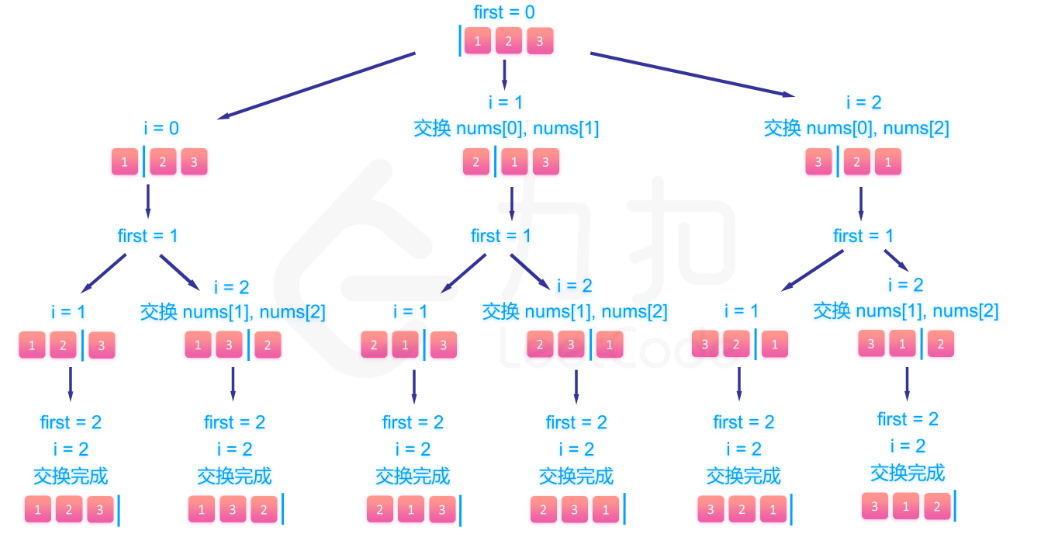

完整代码：

class Solution {
    public List<List<Integer>> permute(int[] nums) {
    	// 首先建立一个返回的集合
        List<List<Integer>> list=new ArrayList<>();
        List<Integer> output = new ArrayList<Integer>();
        // 将输入的数组变成集合
        for (int num:nums){
            output.add(num);
        }
        int n=nums.length;
        // 进入回溯
        backtrack(n,output,list,0);
        return list;
    }

    public void backtrack(int n,List<Integer> output,List<List<Integer>> list,int first){
    // 如果已经到了最后一个，就终止，将当前的数组结构加到集合中
        if (first==n){
            list.add(new ArrayList<Integer>(output));
        }
        for (int i = first; i < n; i++) {
            // 动态维护数组(交换两个集合中任意两个元素（first和i）的位置)
            Collections.swap(output, first, i);
            // 继续递归填下一个数
            backtrack(n, output, list, first + 1);
            // 撤销操作（即撤销上一步中交换的操作）
            Collections.swap(output, first, i);
        }
    }
}

4.2、括号生成问题

leetcode-22

题目：数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

示例1：

1 2	输入：n = 3 输出：["((()))","(()())","(())()","()(())","()()()"]

示例2：

1 2	输入：n = 1 输出：["()"]

提示：

1	1 <= n <= 8

解题思路：
我们可以生成所有 2的2n次方个 ‘(’ 和 ‘)’ 字符构成的序列，然后我们检查每一个是否有效即可。
如果左括号数量不大于 n，我们可以放一个左括号。如果右括号数量小于左括号的数量，我们可以放一个右括号。

完整代码：

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> list=new ArrayList<String>();
        backtrack(list,new StringBuilder(),0,0,n);
        return list;
    }

// open左括号 close右括号
    // max是n的长度
    public void backtrack(List<String> list,StringBuilder sb,int open,int close,int max){

        if (sb.length()==max*2){
            list.add(sb.toString());
            return;
        }

        // 左括号
        if (open<max){
            sb.append('(');
            backtrack(list,sb,open+1,close,max);
            sb.deleteCharAt(sb.length()-1);
        }
        // 右括号
        if (close<open){
            sb.append(')');
            backtrack(list,sb,open,close+1,max);
            sb.deleteCharAt(sb.length()-1);
        }
    }
}

4.3、子集问题

leetcode-78

题目：给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。
解集不能包含重复的子集。你可以按任意顺序返回解集。

示例1：

1 2	输入：nums = [1,2,3] 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例2：

1 2	输入：nums = [0] 输出：[[],[0]]

提示：

1
2
3

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

解题思路：
类似于全排列问题。

完整代码：

class Solution {
    List<List<Integer>> list=new ArrayList<>();
    List<Integer> a=new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        backtrack(nums,0);
        return list;
    }

    public void backtrack(int[] nums,int cur){
        if (cur==nums.length){
            list.add(new ArrayList<Integer>(a));
            return;
        }
        a.add(nums[cur]);
        backtrack(nums,cur+1);
        a.remove(a.size() - 1);
        backtrack(nums,cur + 1);

    }
}